A basic rasterizer which lets you take any image and and fit the parameters of a vector-graphics model to it, using the same techiques that form the backbone of deep learning.
By using signed distance functions (SDF) to represent geometric primitives, and rendering with 1d anti-aliasing, one can get a fully differentiable graphics pipeline. That in turn makes it possible to set up a loss funtion for a rendered image against some reference image, and optimize the rendering parameters to minimize the loss using gradient search techniques. The SDF technique for graphics is not novel, but using it for differentiable 2d-rendering like here was recently described in this paper by Tzu-Mao Li and collaborators
This toolbox shows the concept using the Zygote framework in Julia.
For now circle and triangle primitives are supported, in addition to face-vertex triangle meshes.
Each primitive can be shaded with a linear color gradient which can also be optimized.
To do a basic test, run examples/visualize_circle_recovery.jl
This shows selected iterations when fitting a shaded circle:
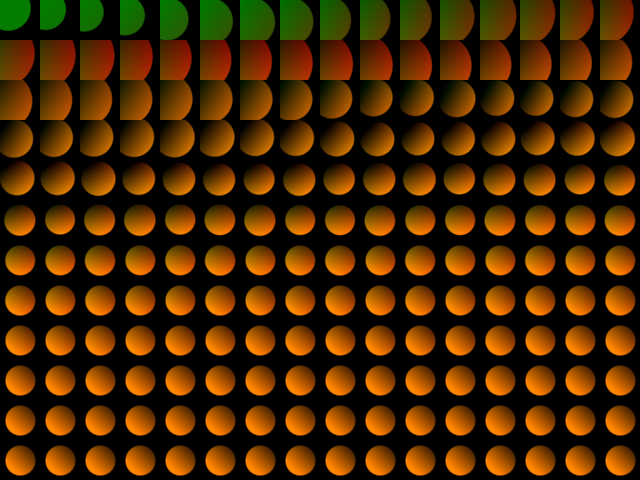
For a more advanced example fitting a triangle mesh to a raster image, run examples/triangle_mesh_optimization.jl
By running for quite a few iterations you should get something like this:

Note that since the vertex positions are unconstrained, the mesh quality may end up being so-so with some very elongated rectangles.
- A better selection of SDF primitives
- Documentation
- Integration with other Julia geometry packages
- Mesh quality regularization
- Tailor for more efficient gradients from Zygote
- Faster rendering with tiles or kD-tree